前馈神经网络(Feedforward Neural Network, FNN),又被称为多层感知机。该网络每层中神经元的输入来源于前一层神经元的输出,并将这层结果输出到下一层神经元。整个网络中,层与层之间的连接都向着同一个方向传播。前馈神经网络的构成要素有:
- 输入层
- 隐藏层的数量(深度 - 1,1代表输出层的数量)
- 隐藏层神经元的个数(宽度)
- 第L层的激活函数
- 第L-1层到第L层的权重向量w
- 输出层
前馈神经网络可以认为是由k个函数嵌套而成的: \(y = f_k...(f_1(x))\)
现在看一下从输入层到第 1 层的第 1 个神经元的信号传递过程:
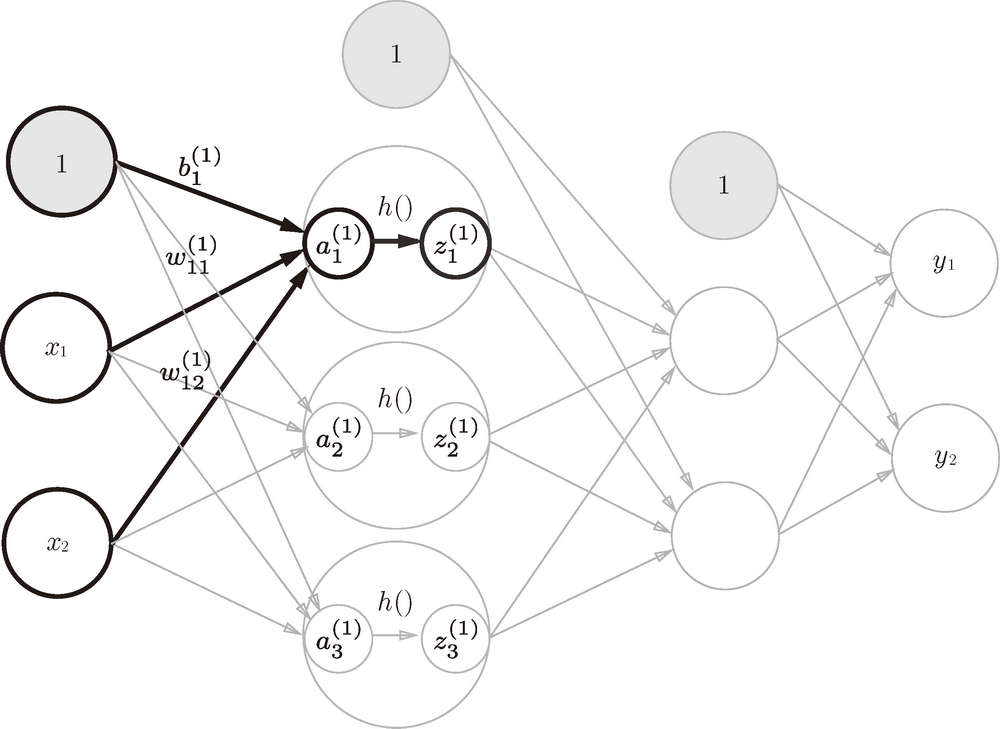
在上图中,第一层的三个神经元可以表示为输入层的加权信号和偏置,然后通过激活函数输出: \(a_1^{(1)} = w_{11}^{(1)}x_1 + w_{12}^{(1)}x_2 + 1\)
\[z_1^{(1)} = h(a_1^{(1)})\]将上面的公式一般化,第L层与第L-1层的关系可以表示为: \(z^{(L)} = f_L(w^{L}z^{(L-1)} + b^{L})\)
激活函数
激活函数用在输出层和隐藏层。其中,常见的有四类非线性的激活函数。
- Sigmoid函数。
它可以使最终输出的值在(0,1),常用于二分类问题,如逻辑回归。 \(y = \frac{1}{1 + e^{(-x)}}\)
对Sigmoid函数求一阶偏导: \(\frac{\partial y}{\partial x} = y(1-y)\)
-
优点:连续可导
-
缺点:存在梯度消失现象。但x很大时,y趋近于1;当x很小时,y趋近于0。这都会使一阶偏导趋近于0,造成梯度消失。
- Tanh函数。
它的输出以0为中心,在(-1,1)。 \(y = \frac{e^z-e^{-z}}{e^z+e^{-z}}\)
对Tanh函数求一阶偏导: \(\frac{\partial y}{\partial x} = 1-y^2\)
- 优点:连续可导
- 缺点:存在梯度消失现象。当x很大时,y趋近于1;当x很小时,y趋近于-1。这都会使一阶偏导趋近于0,造成梯度消失。
- Softmax函数。
它可以使每个类别输出值的总和为1,是逻辑回归在多分类问题的推广。对于多分类问题,类别标签有1,2,…C,共C个类别。给定一个样本,其属于第i类的值被softmax转化为: \(p(y = i|x_i) = \frac{e^{(w_ix_i)}}{\sum_{i=1}^Ce^{(w_ix_i)}}\)
\[其中w_i是第i类的权重向量\]- ReLU函数。
它是目前神经网络中经常使用的激活函数。当x大于0,输出值为x;当x小于等于0时,输出值为0。 \(y = max(0, x)\)
对ReLU求一阶偏导: \(\frac{\partial y}{\partial x} = \begin{cases} 1, & \text {z>0} \\ 0, & \text z \leq 0 \end{cases}\)
- 优点:
- 计算高效,只需加、乘和比较
- 相比Sigmiod函数会导致一个非稀疏的神经网络,RELU函数由于单侧抑制,提供了良好的稀疏性
- 相比Sigmiod函数,缓解了梯度消失问题,并且梯度下降的速度更快。
- 缺点:在训练时,可能会导致神经元死亡的问题。如果参数在一次不恰当更新后,第一个隐藏层中的某个ReLU神经元被置为0,那么这个神经元自身参数的梯度永远都会是0,在以后的训练中永远不能被激活。
激活函数的选择:
- 深度的神经网络,选择Relu。不宜选择Sigmod、Tanh激活函数,因为会导致梯度消失。
- 一般的神经网络,没有限制
通用近似定理
通用近似定理保证了前馈神经网络具有极强的拟合能力。通用近似定理的含义是,只要隐藏层神经元的数量足够,前馈神经网络就可以近似地拟合任意一个给定的连续函数。当然,潜在的问题是如何找到这样一个网络,以及是否是最优的。
误差反向传播算法
在机器学习中,使用梯度下降法对损失函数求偏导,可以求出相应的参数。在前馈神经网络中,如果使用梯度下降法,其复杂度会变得相当高。因为,前馈神经网络的每一个隐藏层都有大量的神经元,这就需要梯度下降法逐一对每个参数求偏导。
根据求导的链式法则,最终的损失函数到权重w1的梯度可以表示为损失函数到神经元h1的偏导与神经元和h1到权重w1的偏导相乘: \(\frac{\partial L}{\partial w_1} = \frac{\partial L}{\partial h_1}\frac{\partial h_1}{\partial w_1}\)
在使用交叉熵损失函数,并用softmax作为激活函数,通过反向传播可以得到如下所示,漂亮的结果: \((y_1-t_1,y_2-t_2,y_3-t_3)\\ 其中,(y_1,y_2,y_3)是Softmax层的输出\\ (t_1,t_2,t_3)是真实标签\)
在回归问题中,使用平方和误差损失函数,恒等函数作为激活函数,反向传播后也能得到上式。
因此,推导可知,第L层的误差项可以由第L+1层的误差项计算得出。误差反向传播算法(BackPropagation,BP),就是基于上述发现来计算参数的。反向传播会从最终的损失值开始,从输出层反向作用到最初层,利用链式法则计算每个参数对损失值的贡献大小,具体可以表示为: \(第L层的一个神经元的误差项 = 所有与该神经元相连的第L+1层的神经元误差项的权重和*该神经元激活函数的梯度。\)
模型的输入与输出
手写数字识别数据集MNIST:每个样本都是高和宽均为28像素的图像,每个像素的数值为0到255之间8位无符号整数。图像为三维数组,由于是灰度图像,其最后一维通道数为1。 \(data_{h,w,c}\)
\[其中h=28, w=28, c=1\]输入:将图像转化为向量,输入向量的长度为28*28=784。 \(X = (a_1,a_2,...,an)\)
\[其中n=784\]模型:由于图像有10个类别,单层神经网络的输出个数也应为10。softmax回归的权重和偏差分别为784X10,1X10的矩阵 \(W_{h,w}\\\)
\[其中h=784,w=10\]输出:1X10的预测概率的矩阵 \(y = (y_1,y_2,...,y_n)\)
\[其中n=10\]