卷积神经网络(Convolutional Neural Network,CNN或ConvNet)是具有局部连接、权重共享、汇聚等特性的深层前馈神经网络。
由于前馈神经网络在处理图像时,存在以下两大问题:
一是第L层有N个神经元,第L-1层有M个神经元,那么最多就会有NXM个连接,这使得参数非常多。通过卷积,则可以降低连接数。
二是图像通过缩放、平移、旋转等操作,不会改变输入的信息。而前馈神经网络很难提取这种局部不变性特征。
卷积神经网络在过去用于图像分类、人脸识别、物体识别、图像分割。近年来,卷积神经网络也广泛地应用于自然语言处理、推荐系统等领域。
卷积神经网络将隐藏层的输入与权重向量进行卷积运算。 \(z^{(L)} = f_L(w^{L}\bigotimes z^{(L-1)} + b^{L})\)
卷积运算:用卷积核分别乘以输入的多维数组(张量)中的每一个元素。
卷积的构成元素有:
- 卷积核。常见的卷积核有Horizontalfiter(检测图像的水平边缘)、Verticalfilter(检测图像的垂直边缘)、Sobel Filter(检测图像的中心区域权重)等。
- 步幅。卷积核在滑动时的间隔
- 填充。在输入向量两端补充零。
卷积神经网络的构成要素有:
- 输入层
- 卷积层
- 探测层:非线性。例如,整流非线性
- 池化层。
- 全连接层
- 输出层
进行卷积核池化的缺陷是可能会导致欠拟合。此外,不适用于对那些依赖于精确空间信息的问题。
卷积层
卷积层具有局部连接和权重共享的性质。
- 局部连接。
- 权重共享。
局部连接的含义是,如果网络中相邻两层之间分别有m个输入和n个输出,那么通过卷积操作,将mXn的参数矩阵减少到了kXn。其中k为卷积核的维度。并且第L层的参数个数为K+1个,与神经元的数量无关。
局部连接的性质天然地吻合图像数据。比如,在人脸识别中,输入的图像包含成千上万个像素点,但我们需要只是鼻子、眼睛、脸等局部的特征。因此,我们通过几十或者几百个像素点就能达到目的。
权重共享指的是卷积核对于第L层的所有神经元都是相同的。权重共享的特性使得卷积层具有平移等变性。当一个函数的输入改变时,输出也以同样方式改变,则我们认为其具有平移等变性。比如对于图像中猫的识别,如果猫在图像中的位置发生了平移,那么相应的输出也会移动相同的量,以保证猫的正确识别。这意味着,不论一只猫出现在图像中的任何位置,我们都能将其识别成猫。
疑问:当处理时间序列数据时,这意味着通过卷积可以得到一个由输入中出现不同特征的时刻所组成的时间轴。如果我们把输入中的一个事件向后延时,在输出中仍然会有完全相同的表示,只是时间延后了。——《深度学习》P207
注:在图像处理中,卷积经常作为特征提取的方法。
池化层
池化是对区域进行滑动求最大值或平均值等操作。这相当于进行特征选择,降低了特征数量。池化的做法,还保持了平移、伸缩、旋转操作的不变性。这种不变性,特别适用于那些我们关心某个特征是否出现,而不关心它出现在哪个位置的情况。
池化层的优点
- 没有要学习的参数
- 通道数不会发生变化
- 对微小的位置变化具有鲁棒性
AlexNet
AlexNet是第一个现代深度卷积神经网络。它使用了GPU进行并行训练,采用ReLU作为非线性激活函数,使用Dropout防止过拟合,使用数据增强(翻转、裁剪和颜色变化)来提高模型准确率。
ResNet
深度残差网络(Deep Residual Network,ResNet)是为了解决或缓解深层的神经网络所出现的梯度消失问题。深度残差网络,在加深神经网络层数的同时,保证了其训练效果。这使得,深度残差网络可以学习到很深层的神经网络。 \(残差网络是做法是让非线性单元f(x;\theta)去近似残差函数h(x)-x,并用f(x;\theta)+x去逼近目标函数h(x)\)
卷积层的输入和输出
对于图像,是具有长、宽、通道的三维数据。全连接神经网络在处理图像数据时,需要把3维拉平为1维数据。而卷积神经网络则可以维持图像的3维形状。
1.二维卷积
输入:每个样本都是高h,宽w的二维数组 \(n_h,n_w\)
卷积核窗口大小: \(k_h,k_w\)
输出的大小: \((n_h-k_h+1),(n_w-k_w+1)\)
卷积的填充。填充将输入的矩阵周围用0填充。填充的目的是改变输出的大小。例如,对于(4,4)的输入,使用(3,3)的卷积核当每次进行卷积时,输出变为(2,2)。这相当于每次进行一次卷积都会减少2个元素。在一个深度的神经网络中,只经过几次卷积操作输出就可能变为1个元素,使得后续无法再应用卷积。因此,通过填充,就可以维持输出的大小。
卷积的步幅。步幅是卷积核在滑动时的间隔。
假设填充为P,步幅为S,那么输出的大小为: \((\frac{n_h-k_h+2P}{S}+1),(\frac{n_w-k_w+2P}{S}+1)\)
2.多输入通道
对于彩色图像数据,除了高和宽之外,还有RGB(红、绿、蓝)三个通道。因此,它可以表示为三维数组,3XhXw。
输入数据:具有高、宽、通道三个参数 \(c_i,n_h,n_w\)
\[当通道数c_i=1时,则是二维卷积的情况\] \[在这里,我们考虑通道数c_i>1的情况\]卷积核窗口大小:要为每一个通道分配一个形状为k_h,k_w的核数组 \(c_i,k_h,k_w\)
\[卷积核数量为c_i\]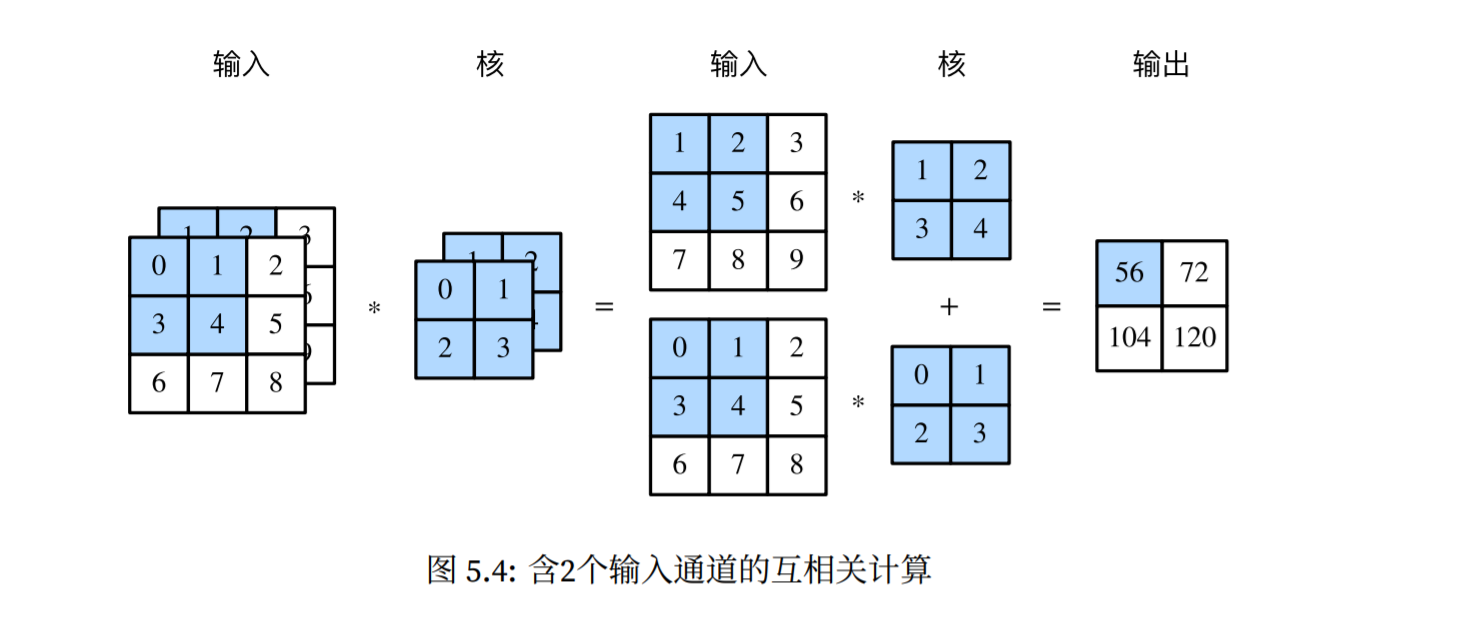
输出:在每个通道上,对输入的二维数组与卷积核的二维数组做互相关运算,然后再将生成的二维数组按照通道累加,得到一个二维数组(通道数变为1)。 \(1,(n_h-k_h+1),(n_w-k_w+1)\)
3.多输出通道
如果要得到多输出的通道,那么需要为卷积核定义一个多输出通道的参数。
输入数据:具有高、宽、通道三个参数 \(c_i,n_h,n_w\)
卷积核窗口大小:拥有输入通道数、输出通道数、长、宽四个参数(batch_num,channel,height,width): \(c_o,c_i,n_h,n_w\)
\[c_o为输出通道数,c_i为输入通道数,n_h为长,n_w为宽\] \[卷积核数量为c_o*c_i\]输出:每个输出通道上的结果由该输出通道上的卷积核与输入数组计算而来 \(c_o,(n_h-k_h+1),(n_w-k_w+1)\)